¿Qué es la Interpolación?	Es hallar una función que pase exactamente por n+1 puntos determinados (6 puntos -> grado 5)
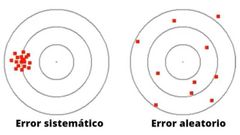
¿Cuáles son las condiciones para que pueda darse una interpolación?	1, Solo se aproximan funciones univaribles 2, Todos los valores de la variable independiente deben ser diferentes. 3, el error aleatorio debe ser despreciable.
¿Para qué hacer una interpolación?	Para saber todos los valores de mi conjunto, es decir, hallar la función que lo describe.
¿Qué son los polinomios de Lagrange?	Son una serie de polinomios que al ser multiplicados por sus f(x), representan la aproximación polinomial de orden n en un punto específico.
¿Cómo es la formula de Lagrange para hallar los polinomios de n puntos?
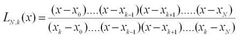
¿Cómo es la formula para hallar la aproximación de los polinomios de Lagrange?
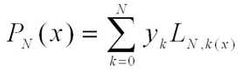
¿Cómo es la formula para hallar la aproximación de los puntos por diferencias divididas de Newton?
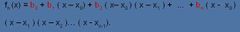
¿Cómo hallo los coeficientes en las diferencias divididas de Newton?	En general es tomar el resultado de las dos diferencias divididas anteriores y dividirlo entre los dos extremos de x.
¿Qué es la interpolación por trazador cúbico?	Es un conjunto de polinomios cúbicos que interpolan una serie de parejas ordenadas (x1, y1), (x2, y2)...
¿Cuál es el conjunto de polinomios que se forma en una interpolación por trazador cúbico?
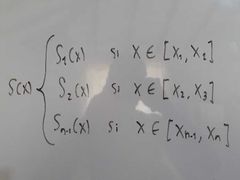
¿Cómo es la forma de un polinomio de trazador cúbico?
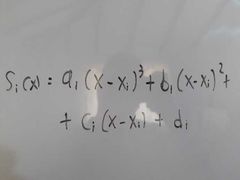
¿Cuál es la cantidad de parámetros que posee un trazador cúbico?	4(n-1)
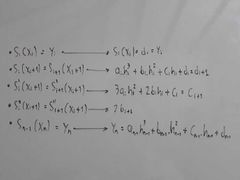
¿Cuáles son las condiciones que deben cumplir los polinomios del trazador cúbico?	El primer valor del polinomio S(i) es el correspondiente di. El final del polinomio S(i) y el comienzo del polinomio S(i+1) debe ser el mismo valor. Las dos primeras derivadas en dicho punto son iguales en los dos polinomios.
¿Cómo se clasifican los tipos de trazadores cúbicos y qué tipos hay?	Se clasifican según las ecuaciones de sus extremos.
¿Qué es el hi en el trazador cúbico?	Es el tamaño del intervalo, es decir: hi= X(i+1)-Xi
¿A qué son iguales los d.i?	d.i = Yi
¿Cómo hallo los b.i de mi trazador cúbico?	Resolviendo el sistema.
¿Cómo hallo los a.i de mi trazador cúbico?
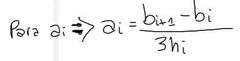
¿Cómo hallo los c.i de mi trazador cúbico?
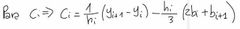
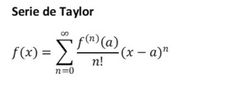
¿Qué me expone el teorema de Taylor?	Me dice que si la función f(x) y sus primeras n+1 derivadas son continuas en un intervalo en el que están contenidos (a) y (x) entonces el valor de f(x) está dado por: mas un residuo Rn.
¿A qué es igual el tamaño de paso h en las series de Taylor?	h = x - a
¿A qué es igual el residuo de las series de Taylor y cómo se va a utilizar?	No se va a evaluar y se va a denotar por la letra O (cota superior asintótica), pero podemos obtener indicios de qué tanto decrece el error al dismuir el tamaño del paso.
¿Qué es la diferenciación numérica?	Son tecnicas para aproximar el valor de una derivada en un valor ESPECIFICO de la variable dependiente. Se conocen como formulas de diferenciación finitas.
¿A qué sería igual la aproximación de una primera derivada por series de Taylor?
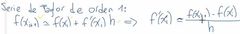
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la primera derivada simple? De sus formulas
¿Cómo son las contracciones para las aproximaciones de las derivadas de primer orden?
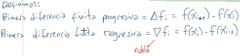
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la Segunda derivada simple?
¿Cómo son las contracciones para las aproximaciones de las derivadas de segundo orden?
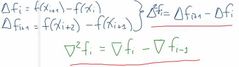
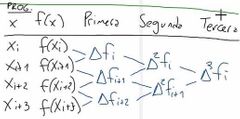
¿Cómo es el proceso para hallar las derivadas de orden n de las derivadas progresivas?	Similar al de las diferencias divididas de Newton:
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la Tercera derivada simple?
¿Cómo se pueden crear mejores aproximaciones de las derivadas que las simples?	Utilizando más terminos de la serie de Taylor.
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la Primera derivada de mayor exactitud?
¿Cómo son los errores de método númerico para las diferencias finitas simples?	En todos los tipos Progresiva Regresiva Central
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la Segunda derivada de mayor exactitud?
¿Cuáles son los tipos de aproximaciones que se pueden hacer de la Tercera derivada de mayor exactitud?
¿Cómo son los errores de método númerico para las diferencias finitas de mayor exactitud?
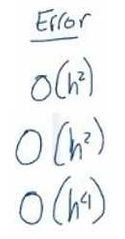
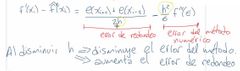
¿Cómo mido el efecto del error de redondeo en una diferenciación?	Con la expresión: de los que se puede intuir que... .
¿Cómo se mide la estabilidad de un algoritmo y de qué tipo son las diferencias finitas?	Lo mido a partir de los cambios pequeños en la variable de entrada, si estos producen siempre cambios pequeños se dice que es ESTABLE, de lo contrario es INESTABLE. Las diferencias finitas son inestables.
¿Cuando expreso delta y cuando nabla?	Delta: Si hago un cambio hacia adelante de la variable que estoy estudiando. Nabla: Si hago un cambio hacia atras de la variable que estoy estudiando.