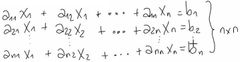
¿Qué es un sistema de ecuaciones lineales?	Es un conjunto de ecuaciones lineales que son combinaciones lineales de las variables.
¿Qué es una matriz?	Es un arreglo rectangular de elementos.
¿Qué es una matriz cuadrada?	Es una matriz con igual número de filas y columnas.
¿Qué es la diagonal principal?	Es el conjunto de elementos de la matriz fomada por los a.i,j en los que i=j.
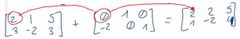
¿Cómo se hace una suma o resta de matrices y que restricciones tiene?	Solo se puede aplicar entre matrices de igual dimensión n×m Consiste en sumar el elemento a.i,j con el elemento de la otra matriz b.i,j.
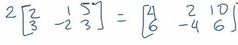
¿En qué consiste la multiplicación de una matriz por un escalar?	Como tal es multiplicar cada elemento de la matriz por un escalar.
¿Qué tipos especiales de matrices cuadradas hay?	Simétrica Diagonal Identidad
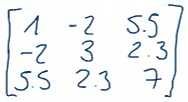
¿Qué es una matriz simétrica?	Es aquella en la cual los a.i,j = a.j,i.
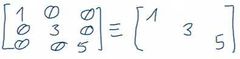
¿Qué es una matriz diagonal?	Es una matriz en la cuál todos los elementos, excepto los de la diagonal principal son cero.
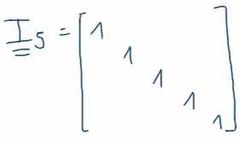
¿Qué es una matriz identidad?	Es una matriz solo con unos en la diagonal principal.
¿Qué es una matriz triangular y qué tipos hay?	Es una matriz en la que todos los elementos a un lado de la diagonal principal son cero. TIPOS Inferior: encima de la diagonal principal. Superior: debajo de la diagonal principal.
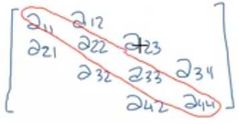
¿Qué es una matriz Tridiagonal?	Es una matriz en la cual los únicos elementos diferentes de cero están en la diagonal principal y las dos diagonales contiguas a ella.
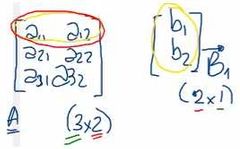
¿Qué se necesita para poder hacer una multiplicación entre las matrices A y B?	Es necesario que el número de columnas de A sea igual al número de filas de B para hacer AB. € si A(m×n)B(n×s)
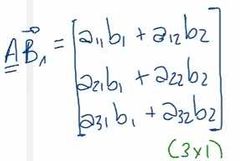
¿Cómo es la matriz C producto de A*B?	Cada elemento i,j de la matriz C es la suma del producto de los elementos individuales de la i-esima fila de A y la j-esmina columna de B.
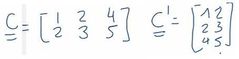
¿En qué consiste la transposición de una matriz?	Consiste en intercambiar la fila y la columna de los elementos de la matriz.
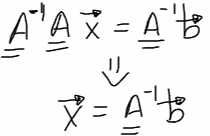
¿Cómo se hace una división de matrices?	La división de matrices no existe, pero se puede simular la división multiplicando a la matriz por la inversa de la otra.
¿Cómo es la representación matricial de un sistema lineal?
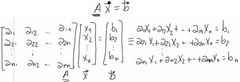
¿Qué puedo saber a partir del determinante de una matriz?	Si det(A) ~=0, entonces se cumple: 1, Ax = 0 tiene como unica solución x = 0. 2, Ax = b tiene única solución para cualquier vector n-dimensional b. 3, A no es singular, es decir, tiene inversa.
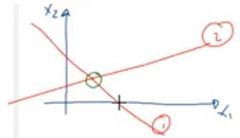
¿En qué consiste el método gráfico?	En si es gráficar las funciones (ecuaciones del sistema) y determinar que punto tienen en común todas.
¿Cuáles son las operaciones que se pueden hacer a un sistema lineal y no lo alteran?	1, Intercambiar de posición las ecuaciones. 2, Multiplicar una ecuación por una constante. 3, Combinar linealmente dos ecuaciones y sustituir una de las dos ecuaciones por la combinación lineal.
¿En qué consiste la Eliminación de Gauss-Jordan?	El objetivo es aplicar eliminación para obtener una ecuación con una incognita, una con dos, para resolver secuencialmente.
¿Qué pasos encierra la eliminación de Gauss?	1, Eliminación (obtener matriz triangular) 2, Sustitución hacia atrás (hallar los valores de las variables)
¿En qué consiste el método de Gauss-Jordan?	En si es utilizar la eliminación para llegar a la matriz identidad.
¿Qué es el condicionamiento de un sistema?	Es medir la sensibilidad para saber si el resultado es lo suficiente robusto cuando se hacen pequeños cambios en las entradas para evitar problemas en los redondeos.
¿Qué se puede hacer si un sistema está mal condicionado?	1, Escalar el sistema d modo que para la ecuación i, el a.i,j mas grande sea uno. 2, Reordenar las ecuaciones, buscando que los valores más grandes (en magnitud) esten en la diagonal principal. 3, Recalcular det(A).
¿Qué es la descomposición LU?	Es un método analítico, en el cual se usa como paso intermedio la descomposición de la matriz A a la L(Lower) y U(upper).
¿Qué ecuaciones describe la descomposición LU?	Ya que en la etapa intermedia de eliminación de Gauss se convierte en:
¿A qué es igual la matriz U?	A la matriz A después de aplicarsele ls Eliminación Gaussiana.
¿A qué es igual la matriz L?	Son los factores utilizados para volver 0 el elemnto en la misma posición de la matriz A.
¿Cómo se halla el vector d de la descomposición LU?	Mediante sustitución hacia atras.
¿Cómo resuelvo el sistema con la descomposición LU?	Mediante la sustitución hacia atras.
¿Mediante que métodos puedo hallar la inversa de una matriz?	1, Gauss Jordan (aplicando las operaciones de A a la matriz identidad). 2, Descomposición LU
¿Qué me expresa la inversa de una matriz?	Cada elemento de la inversa representa el cambio en una de las variables ocasionadas por un cambio unitario en un valor en un valor del vector de términos independientes.
¿Cómo se puede saber si un sistema está mal condicionado?	1, Escalar A de manera que el coeficiete más grande en cada fila sea 1, Invertir A, Si en 1/A hay elementos varios órdenados de magnitud superior a la unidad, está mal escalada. 2, Multiplicar A por 1/A si la respusta difiere mucho de I, está mal condicionada. 3, Invertir 1/A, Si ls respuesta difiere mucho de A, está mal condicionada.