¿Què es un vector?	Un vector es todo segmento de recta dirigido en el espacio.
¿Què es el origen?	O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
Módulo	Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección	Viene dada por la orientación en el espacio de la recta que lo contiene.
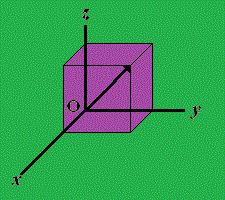
Sentido	Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector
Magnitudes Escalares	Denominamos Magnitudes Escalares a aquellas en las que las medidas quedan correctamente expresadas por medio de un número y la correspondiente unidad.
Magnitudes vectoriales	Las magnitudes vectoriales son magnitudes que para estar determinadas precisan de un valor numérico, una dirección, un sentido y un punto de aplicación.
Vector	Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir: * Un origen o punto de aplicación: A. * Un extremo: B. Una dirección: la de la recta que lo contiene. Un sentido: indicado por la punta de flecha en B. *Un módulo, indicativo de la longitud del segmento AB.
Vectores iguales	Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección.
Vector libre	Un vector libre queda caracterizado por su módulo, dirección y sentido. El vector libre es independiente del lugar en el que se encuentra.
Propiedades de vectores	Conmutativa: a+b=b+a Asociativa: (a+b)+c=a+(b+c) Elemento Neutro: a+0=a Elemento Simétrico: a+(-a)=a-a=0
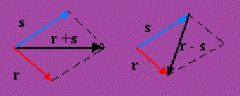
Suma y resta de vectores	La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma: Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo. Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.
La suma de vectores goza de las siguientes propiedades:	Conmutativa a + b = b + a Asociativa (a + b) + c = a + (b + c) Elemento neutro o vector 0 a + 0 = 0 + a = a Elemento simétrico u opuesto a' a + a' = a' + a = 0 a' = -a
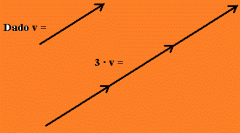
Producto de un vector por un escalar	El resultado de multiplicar un escalar k por un vector v, expresado analíticamente por kv, es otro vector con las siguientes características : 1.- Tiene la misma dirección que v. 2.- Su sentido coincide con el de v, si k es un número positivo, y es el opuesto, si k es un número negativo. 3.- El módulo es k veces la longitud que representa el módulo de v. ( Si k es 0 el resultado es el vector nulo).
Propiedades del producto de un vector	El producto de un vector por un escalar cumple las siguientes propiedades: 1.- Conmutativa: k · v = v · k. 2.- Distributiva: k (v + u) = (k · v ) + (k · u). 3.- Elemento Neutro: 1 · v = v. 4.- Elemento Simétrico: -1 · v = - v.
Producto escalar de dos vectores	El producto escalar de dos vectores, expresado analíticamente como r · v, se obtiene de la suma de los productos formados por las componentes de uno y otro vector. Es decir, dados dos vectores r y v, expresados en un mismo sistema de coordenadas: r = rxi + ryj + rzk v = vxi + vyj + vzk
Propiedades	Conmutativa : r · v = v · r Distributiva : r · ( v + u ) = r · v + r · u Asociativa : ( k · r ) · v = k · ( r · v ) = r · ( k · v ) siendo k escalar. Además : 1.- r · r = 0 si, y sólo sí r = 0. 2.- Si r y v <> 0 y r · v = 0, esto implica que los vectores son perpendiculares, (cos 90º = 0). 3.- El producto escalar de dos vectores es equivalente a multiplicar escalarmente uno de ellos por el vector proyección del otro sobre él.
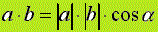
Producto escalar	El producto escalar de dos vectores es por definición un escalar.
Propiedades:
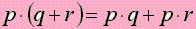
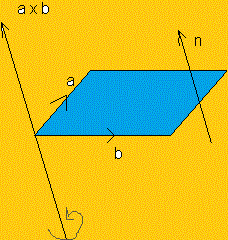
Producto vectorial	El producto vectorial de los vectores a y b, se define como un vector, donde su dirección es perpendicular al plano de a y b, en el sentido del movimiento de un tornillo que gira hacia la derecha por el camino más corto de a a b, se escribe axb
Propiedades:
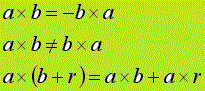
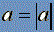
Módulo de un vector	Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa magnitud se le denomina módulo.