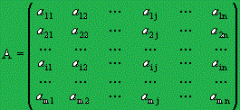
¿Què es una Matriz?	es el arreglo rectangular en filar (o renglones) y columnas
elementos de una matriz	Cada uno de los números de que consta la matriz se denomina elemento. Un elemento se distingue de otro por la posición que ocupa, es decir, la fila y la columna a la que pertenece.
Dimensión de una matriz	El número de filas y columnas de una matriz se denomina dimensión de una matriz. Así, una matriz de dimensión mxn es una matriz que tiene m filas y n columnas. El conjunto de matrices de m filas y n columnas se denota por Amxn o (aij). Un elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j, se denota por aij.
tipos de matrices	* Matrices iguales Matriz fila Matriz columna Matriz rectangular Matriz traspuesta Matriz nula Matriz cuadrada
Matrices iguales	Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas, son iguales.
Matriz fila	Una matriz fila está constituida por una sola fila.
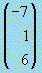
Matriz columna	Matriz columna
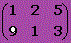
Matriz rectangular	La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.
Matriz traspuesta	Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas. -(A + B)t = At + Bt -(α ·A)t = α· At -(A · B)t = Bt · At
Matriz nula	Matriz nula
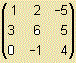
Matriz cuadrada	La matriz cuadrada tiene el mismo número de filas que de columnas. Los elementos de la forma aii constituyen la diagonal principal. La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.
Tipos de Matrices cuadradas	Matriz triangular superior Matriz triangular inferior Matriz diagonal Matriz escalar *Matriz identidad o unidad
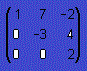
Matriz triangular superior	En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.
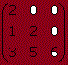
Matriz triangular inferior	En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.
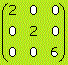
Matriz diagonal	En una matriz diagonal todos los elementos que no están situados en la diagonal principal son nulos.
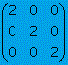
Matriz escalar	Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
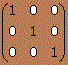
Matriz identidad o unidad	Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.
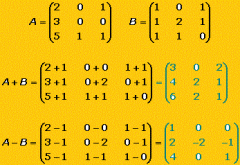
Suma de matrices	Dadas dos matrices de la misma dimensión, A = (aij) y B = (bij), se define la matriz suma como: A + B = (aij + bij) La matriz suma se obtiene sumando los elementos de las dos matrices que ocupan la misma posición.
Propiedades de la suma de matrices	1. Interna 2. Asociativa 3. Elemento neutro 4. Elemento opuesto 5. Conmutativa
Interna	La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
Asociativa	A + (B + C) = (A + B) + C
Elemento neutro	A + 0 = A Donde O es la matriz nula de la misma dimensión que la matriz A.
Elemento opuesto	A + (−A) = O La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
Conmutativa	A + B = B + A
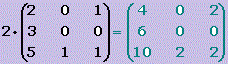
Producto Escalar	Dada una matriz A = (aij) y un número real k perteneceR, se define el producto de un número real por una matriz: a la matriz de la misma dimensión que A, en la que cada elemento está multiplicado por k. k · A = (k · aij)
Propiedades del Producto Escalar	Distributiva Modulativa Conmutativa NO HAY LEY ASOCIATIVA
Distributiva	a · (A + B) = a · A + a · B
Modulativa	1 · A = A
Conmutativa	a · (b · A) = (a · b) · A
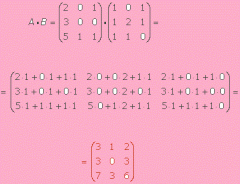
Producto de matricez	Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B. El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.
Propiedades de productos de matrices	1 Asociativa: A · (B · C) = (A · B) · C 2 Elemento neutro: A · I = A Donde I es la matriz identidad del mismo orden que la matriz A. 3 Distributiva del producto respecto de la suma: A · (B + C) = A · B + A · C 4 No es Conmutativa: A · B ≠ B · A
Matriz inversa	Si premultiplicamos (multiplicamos por la izquierda) o posmultiplicamos (multiplicamos por la derecha) una matriz cuadrada por su inversa obtenemos la matriz identidad. A · A−1 = A−1 · A = I
Propiedades	1 (A · B)−1 = B−1 · A−1 2 (A−1)−1 = A 3 (k · A)−1 = k−1 · A−1 4 (At)−1 = (A−1)t
Metodo de Gauss	Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A−1