¿Que es una magnitud escalar?	Es aquella que queda definida con solo indicar su cantidad expresada en números y la unidad de medida.	Son magnitudes de la vida diaria como el Kg, los Grados C°, la longitud, el tiempo etc.
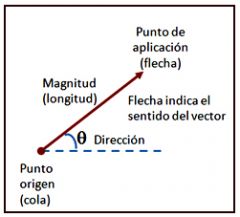
¿Que es una magnitud vectorial, cuales son los elementos de un vector y como se pueden representar?	Son aquellas magnitudes que para definirse además de la cantidad expresada en números y el nombre de la unidad , necesita que se señale la dirección y el sentido. Todo vector tiene 1.punto de aplicación; 2. Magnitud; 3. Dirección; 4. Sentido. Se puede representar de forma "Polar" o en un sistemas de "coordenadas".	Son magnitudes como el desplazamiento, velocidad, aceleración, fuerza, etc.
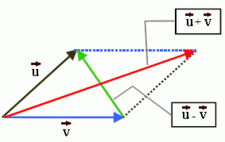
Suma y resta de vectores	V1+V2= (V1x+V2x,V1y+V2y) donde a y b son los componentes en el plano cartesiano, o bien se puede utilizar el método del paralelogramo.	Paralelogramo
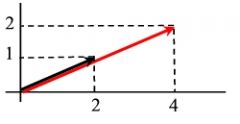
Producto de un escalar por un vector	V = (2,1) k = 2 k V = 2 (2, 1) = (4, 2) V=vector k=escalar	El vector se incrementa las veces del escalar
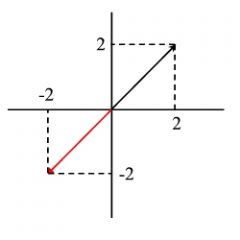
Producto de -1 por un vector	V= (2, 2) k = -1 k V = -1 (2, 2) = (-2, -2)	invierte el sentido
vector unitario	relación entre el vector y su magnitud
Vectores en tres dimensiones
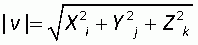
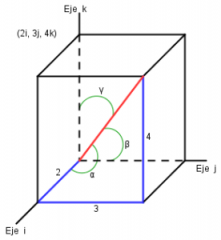