¿Qué es una relación?	Es el hecho de que un elemento de un conjunto se relacione con otro elemento de otro conjunto. Ejemplo Pájaro Caminar Perro Volar Pez Nadar Serpiente Pájaro= caminar y volar Perro= Caminar y nadar Pez= Nadar Serpiente=
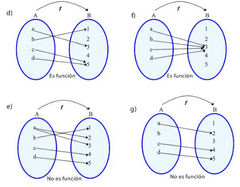
¿Qué es una función?	Es un tipo de relación entre dos conjuntos X y Y en el que a CADA elemento de X le corresponde un ÚNICO valor en Y. Es una función si: Cada elemento de x está relacionado con uno Y SOLO uno en Y, no importa que un elemento de Y reciba varias flechas, lo que importa es que todos en X les salga SOLO una flecha NO es función si: 1. Un elemento en x se queda sin relacionar. 2. Si sale más de una flecha en un elemento de x
¿Cuál es el conjunto de llegada y cuál es el conjunto de partida?	El conjunto de partida siempre es X ya que de ahí es que salen las flechas, mientras que el de llegada es Y ya que él recibe esas flechas
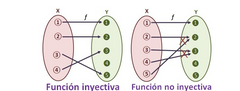
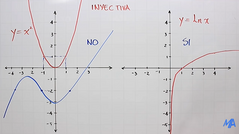
TIPOS DE FUNCIONES: 1nyectiva	1nyectiva o uno a uno Que a cada elemento de Y le llegue solo 1 flecha o ninguna. Y ¿Cómo se ve en una gráfica? Los elementos de X serían el conjunto X y los elementos de Y serían el conjunto Y. Entonces Si la gráfica sube y vuelve a bajar o baja y vuelve a subir NO ES INYECTIVA porque a un elemento de y le llegan 2 flechas de x. Si sube y sube y no baja o baja y baja pero no vuelve a subir es porque SI ES INYECTIVA Un truco para saber si es inyectiva es trazar una recta completamente horizontal y ver si solo corta una vez a esa recta, si sí es porque es inyectiva, si la corta en dos puntos es porque no es inyectiva y ¿Pasa algo si a un elemento en Y no le llega flecha? No, sigue siendo función inyectiva y ¿Si a un elemento en y le llega más de una flecha pero otro elemento en y se queda solo? Ahí NO es inyectiva, no porque un elemento quede solo sino porque a un elemento le llegaron dos flechas
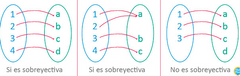
TIPOS DE FUNCIONES: Sobreyectivas Memotencia: No sobra Y	Que a CADA elemento en Y le llegue al menos 1 flecha de x, o sea que no sobren elementos en Y. Si tengo 1 2 3 a 4 Todos los número se relacionan con a: 1a, 2a, 3a, 4a Y como a todos los números de x les salió una flecha es función y como a todos los elementos de Y (solo a en este caso) les llego una flecha es sobreyectiva Y cómo se ve en el plano. Una función cuadrática nunca será sobreyectiva porque habrán elementos en y que sobren, y eso no se puede en las sobreyectivas porque NO PUEDEN SOBRAR ¿Una recta sería una función sobreyectiva? Sí, porque cubre a todos los elementos en Y https://www.youtube.com/watch?v=-9sJnBLJxKI&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=2 MIN 9:50
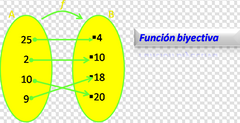
TIPOS DE FUNCIONES: Biyectiva	Que es 1nyectiva y sobreyectiva al mismo tiempo. O sea que la relación entre los elementos de X y Y es uno a uno y en Y no puede sobrar ni un elemento ¿Una recta sería biyectiva? Sí, porque es inyectiva y sobreyectiva al mismo tiempo, su relación entre los elementos de X y Y es uno a uno y no sobra ninguno en Y ¿Las funciones racionales son biyectivas? Depende de como este dibujada. https://youtu.be/-9sJnBLJxKI MIn 17:30
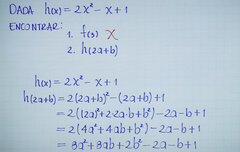
Cómo evaluar o encontrar una función	Por ejemplo me dan la ecuación f(x)=3x-2 y me piden hallar cuando f(-3) y f(2) Entonces reemplazo las x por esos números f(x)=3x-2 f(x)=3(-3)-2 f(x)=-9-2 f(x)= -11 Entonces el intervalo será (-3,-11) porque cuando x vale -3, f(x) o y valdrá -11 f(x)=3(2)-2 f(x) =6-2 f(x)=4 Intervalo (2,4)
¿Y si me llegan a dar la ecuación g(x)=5x²-2x+1 con f(3) y f(-2)?	No se puede realizar, ya que f(x) y g(x) NO son lo mismo Pero si fuese g(3) y g(-2) sí. O si fuese f(x)=5x²-2x+1 también se podría. Y simplemente se reemplazaría la x por esos valores
Y si tengo por ejemplo f(x)=3x-5 con f(x+1)	Entonces x=(x+1) así que reemplazamos donde diga x por eso f(x+1)=3(x+1)-5 f(x+1)=3x+3-5 f(x+1)=3x-2 Y listo
Y si tengo por ejemplo h(x)=2x²-x+1 donde h(2a+b)	Reemplazo h(2a+b)=2(2a+b)²-(2a+b)+1 h(2a+b)=2((2a)²+2(2a)(b)+b²)-(2a+b)+1 h(2a+b)=2((4a²)+4ab+b²)-2a-b+1 h(2a+b)=8a²+8ab+2b²-2a-b+1 Y así queda
Dominio y rango de una función	El dominio son los valores que toma una función en el eje x mientras que el rango son los valores que toma en Y.
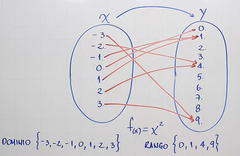
Dominio y rango en la forma de dos conjuntos x y Y	Si tenemos dos conjuntos f(x)=x² -3 0 -2 1 -1 2 0 3 1 4 2 5 3 6 El dominio sería todos los números del conjunto x de los que salen flechita (aquí no se ve pero en el cuaderno rosado hice el mismo ejercicio) Y el rango serían únicamente los números a los que le llegaron flechita https://www.youtube.com/watch?v=H40lcwlgPMk&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=8
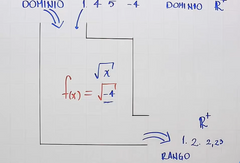
Dominio y rango de función en su forma analítica	Por ejemplo F(x)=√x Entonces el dominio son todos los números a los que les puedo sacar raíz y el rango sería esa raíz resuelta F(x)=√x Dominio= 1,2,3,4,5... Rango= 1, √2, √3, 2, √5... ¿-4 puede ser parte del dominio? No porque no existen las raíces negativas https://www.youtube.com/watch?v=H40lcwlgPMk&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=8
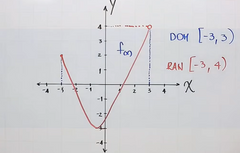
Dominio y rango en gráfica	Dominio= Desde donde inicia la gráfica en el eje x de izquierda a derecha hasta donde termina. Rango= Desde donde inicia en el eje Y de abajo hacia arriba hasta donde termina. https://www.youtube.com/watch?v=H40lcwlgPMk&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=8
y= 5 y= 3 --------- x y=x y=√x y=6x Son funciones lineales?	y=5 Sí, es una función lineal completamente horizontal con pendiente cero y=x sí, es una función lineal oblicua creciente y= 3 NO es una función LINEAL, la x no puede ir ------ en el denominador, es función raciona x y=√x No es una función lineal, la x no puede ir en una raíz, pero no sé que tipo de función sea y=6x sí es función lineal y su corte en y sería cero.
Tipos de funciones lineales	Oblicuas: La creciente y decreciente, tienen la letra x sí o sí. Si no tienen corte en y pues la recta pasa por cero en el eje Y Horizontal: sería por ejemplo y=3, con x a la cero, por tanto su pendiente es cero y solo tendría el corte con Y que sería ese número. Vertical NO existe. No hay funciones completamente verticales
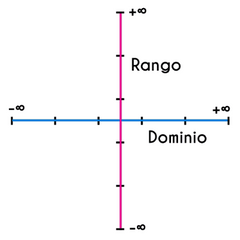
Dominio y rango de una función lineal	Solo hay funciones lineales completamente horizontales u oblicuas. Entonces en horizontales. El dominio como son los valores de X serían todos los reales, mientras que el rango sería un solo número. El número que nos den. Si nos dan por ejemplo y=9 El dom= R El Ran= 9 Ya que 9 es el único número por el que pasa la recta en el eje Y, es su punto de corte y por tanto su rango Por otro lado. En cuanto a las oblicuas, ellas deben tener si o sí a x en su función. Si no tienen corte en y, o sea si son y=3x o algo parecido significa que su corte en y es en el punto cero. Entonces su dominio serían todos los reales y su rango también ya que son rectas que no tienen fin. https://youtu.be/G-sduIBzvVU Min 6:40
¿Cómo se halla el vértice de una parábola?	V((-b/2a),y) Se sabe que el vértice es el punto más alto o más bajo de la curvatura de una parábola entonces si tenemos por ejemplo 2x²-8x+6 Para hallar a x usamos -b/2a Sabemos que a=1, b=-8 y c=6 Entonces -8/2(2)= 8/4=2 Entonces x= 2 Mientras que para hallar a Y lo que hacemos es reemplazar ese valor de x en la función 2(2)²-8(2)+6 2(4)-16+6 8-16+6=y -2=y Y el vértice queda (2,-2)
Cómo graficar una función cuadrática	Nos dan la función y=2x²-4x-1 Entonces lo primero es hallar el vértice, primero x y luego reemplazamos x= -b/2a= 4/4=1 X=1 y=2(1)²-4(1)-1 y=2-4-1 y= -3 Vértice= (1,-3) Ahora lo que hacemos es una tabla de valores con diferentes valores para x, preferiblemente hacerla con 5 valores
Dominio y rango de una función cuadrática	El dominio siempre serán todos los reales El rango sería desde el punto del vértice hacia arriba o hacia abajo dependiendo de hacia donde abra
Cuáles son funciones cuadráticas	y=x² SI y= x² NO pq hay x ------ en el y=2x²-5 SI 3x denominador y= (x+3)²-2 SI y=5x²-3x-5x² No porque 5x²-5x²=0 y=3x²-2x³
Qué representan a, b y c en una ecuación cuadrática	si tenemos ax²+bx+c a= Si es positiva abre hacia arriba, y si es negativa abre hacia abajo b= si es positiva se mueve en x a los negativos, si es negativa se mueve en x a los positivos c= se mueve en el eje y, si es positiva hacia arriba, si es negativa hacia abajo
Función racional	Se sabe que una función es racional si en el denominador está la x. Por ejemplo 2x-5 ---------- x-3 Y si está en el denominador pero no en el numerador? Igual es racional Y si está en el numerador pero no en el denominador? NO es racional, ahí sería lineal o cuadrática dependiendo de si está a la 1 o al cuadrado
Cómo graficar una función racional	Primero hay que dibujar las asíntotas que son rectas, una vertical y la otra horizontal Entonces si tenemos por ejemplo 2x-5 ------- x-3 Sabemos que el denominador jamás puede ser cero así que x-3≠ 0 Despejamos x x≠ 3 Así que x jamás puede tomar el valor de 3, entonces hacemos una línea en ese número de manera vértical Ahora si la x del numerador y la x del denominador tienen el mismo exponente usamos esto para hallar la horizontal Número que acompaña x en numerador -------------------------------------------------------------- Número que acompaña a x en denominador Ejemplo 2 ----- = 2 1 Entonces hacemos una línea horizontal en el punto 2 del eje Y. Ahora se buscan los puntos de corte con los ejes para saber de que lado va cada curva. Entonces lo que hacemos es reemplazar la Y por cero 0= 2x-5 ---------- x-3 Entonces el denominador (x-3) pasará a multiplicar a cero 0=2x-5 Ahora despejamos x 5 ---- = x 2
Cómo graficar una función racional parte2	Después de hallar el punto de corte con el eje x ahora lo hacemos con el eje Y reemplazando las x por ceros y= 2(0)-5 -5 5 ------------ = ------------ = ------ 0-3 -3 3 Así sabemos como hallar una de las curvas, sin embargo es más fácil con tabla de valores. Simplemente reemplazamos a x con los valores más cercanos a las asintotas
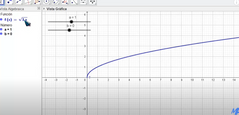
Y si tengo una función en una raíz	La función se verá así. https://youtu.be/4DIk2WiVv44 Para hallar el dominio sabemos que el radicando no puede ser negativo entonces decimos que lo que esta dentro de la raíz es mayor o igual a cero, por ejemplo √x-6 Ponemos el radicando x-6 igual o mayor a cero x-6 > = 0 Y despejamos x x > = 6 Entonces x solo puede tomar valores mayores o iguales a 6
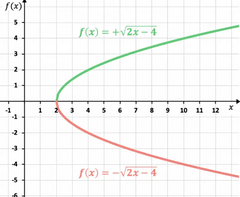
Y si el índice de la raíz es negativa cómo se vería la función	Se vería como si estuviera reflejada en el eje así
¿Qué requisitos tiene una función exponencial además de lo obvio?	Que su base no puede ser negativa, es decir no puede ser por ejemplo (-3) a la x, pero si - 3 a la x, esto porque en el primer caso el - esta dentro de la base y el exponente lo afecta pero en el segundo caso el menos esta aparte del 3, siendo el 3 la base Que su base NO puede ser igual a 1 debido a que sería una línea recta horizontal
QUE TENER EN CUENTA CON LAS FUNCIONES EXPONENCIALES	Que siempre van a cortar en el eje y al número 1
Como hallar las soluciones de una ecuación sin c	Es decir si tenemos por ejemplo la ecuación x² +4x Entonces factorizamos por factor común quedando x(x+4)=0 Y ahora que uno de los dos términos pase a dividir x=0/(x+4) x=0 Y luego el otro (x+4)= 0/x =0 x+4=0 x=0-4 x= -4 Otro ejemplo 2x² -12x=0 2x² -12x=0 2x (x-6)=0 2x (x-6)=0 2x=0/(x-6) x-6=0/2x x=0 x=6 Entonces las dos soluciones de esta ecuación son cero y 6
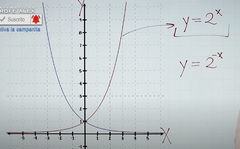
Transformaciones funciones exponenciales: CAMBIO DE SIGNO EN EL EXPONENTE	Si tengo por ejemplo y= 2 a la x me describirá una función Y su cambio de signo en el exponente sería y= 2 a la -x Sería como un reflejo de esa función https://youtu.be/gea1Wz-yMC0 MIN 3:38 a 5:40
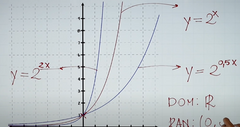
Transformaciones funciones exponenciales MULTIPLICANDO AL EXPONENTE	Si se multiplica el exponente por un número más grande que 1 entonces será más levantadita la función. Si se multiplica por un número menor a 1 será más acostadita
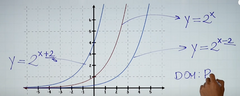
Transformación de funciones exponenciales SUMA O RESTA AL EXPONENTE	Si se le suma se corre el gráfico para la izquierda a los negativos. Si se le resta se corre el gráfico a la derecha a los positivos. Nota: Si te fijas al exponente al que se le suma o resta ya no pasa por el número 1 en y
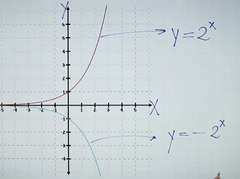
Transformación de funciones exponenciales: Cambio de signo a la base sin el paréntesis porque con paréntesis no se puede xd	En este caso la función se refleja con respecto al eje x
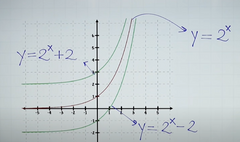
Transformación de funciones exponenciales Suma o resta a la base	En este caso si se resta la función bajaría con respecto al eje y la cantidad de unidades que diga Y si se suma la función subiría con respecto al eje y la cantidad de unidades que diga
Entre más grande sea la base de una función exponencial	Más levantadita es, pero siempre pasa por 1
FUNCIÓN LOGARITMICA Cómo se ve y forma algebraica	Es curveada pero no como la radical ya que inicia en menos infinito, como un palito con su curvita Y en cuanto a su forma algebraica es f(x)= log en base algo (ax+b) Por ejemplok f(x)= log en base 2 de (3,2x+1,5) f(x)=log (8x+2)
Función logarítmica Si se cambia la base a un número más grande...	...La curva es menos curvada xd, es más plana
Función logarítmica Si se cambia el número dentro del paréntesis CON la X...	... a un número más grande se mueve al lado positivo de Y O sea que entre más pequeño el número más baja PERO CUANDO ES NEGATIVO la función se voltea con respecto a Y, como cuando en la función exponencial el exponente se vuelve negativo y se voltea la función en Y, así.
Función logarítmica Si se cambia el número dentro del paréntesis sin la x	Si se vuelve más grande se mueve en el eje x hacia los negativos Si se vuelve más pequeño se mueve en el eje x hacia los positivos
¿Qué tener en cuenta con el paréntesis de una función logarítmica?	Que nunca puede ser negativo
Cómo saber si una función es par	Es simétrica al eje Y Es decir que el lado de la izquierda del eje Y es igual al lado de la derecha, o sea es como si la parte derecha fuese un reflejo de la izquierda o viceversa f(x)=f(-x) TENER MUY EN CUENTA https://www.youtube.com/watch?v=UlD9kTKo7c8&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=21
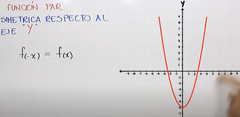
¿Qué significa f(x)=f(-x) en funciones pares?	Que si tu miras en una función par, por ejemplo el punto 2 y el punto -2 la parábola estará exactamente igual en ambos puntos https://www.youtube.com/watch?v=UlD9kTKo7c8&list=PLeySRPnY35dGfEuNGbQmymhiQF4oTUIMb&index=21
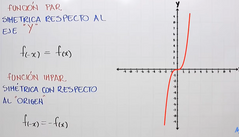
Función impar	Es simétrica con respecto al origen, o sea es como si la dobláramos dos veces, primero con respecto a y y luego con respecto a x. De modo que si inicio en el cuadrante 1 por ejemplo termine en el cuadrante 3 PERO HAY OTRO TIPO DE FUNCIÓN IMPAR Y ES LA CÚBICA
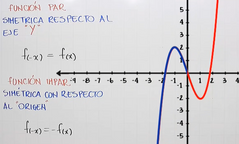
FUNCIÓN IMPAR CÚBICA	Sabemos que es impar, pero gráficamente vemos que si doblamos la parte roja al otro lado de Y y luego al otro lado de X nos da lo de la imagen. Ahora con respecto a f(-x)= - f(x) Para f (-x) simplemente elegimos un valor de x negativo, puede ser el -1 y vemos a que altura está la gráfica para ese punto y nos damos cuenta de que es 2 Con -f(x), buscamos un valor de x cualquiera, como ahorita buscamos -1 entonces ahora buscaremos en 1 f(1) a qué altura está? A -2 pero no nos piden f(1), nos piden -f(1), entonces como f(1) es -2 colocamos - -2 y menos por menos es más entonces f(-x)=-f(x) 2=2
Y si no es par o impar?	Se dice que no tiene paridad
Y numéricamente como se si es par	Par: Nos van a dar una función f(x)=2x²-3 Entonces ya tenemos la mitad que es f(x), ahora falta f(-x) así que lo que hacemos es solo reemplazar donde diga x con -x quedando f(-x)=2(-x)²-3 f(-x)= 2x-3 Se comprueba que f(-x)= f(x) Y se sabe que es par
Y numéricamente como se si es impar	Por ejemplo nos dan f(x)= x³-2x Entonces primero reemplazamos la primera parte f(-x) f(-x)= (-x)³-2 (-x) f(-x)= -x³ +2x Y ahora la segunda parte que es multiplicar la expresión del inicio con un negativo -f(x)= x³-2x (-) -f(x)= -x³+2x Se comprueba que -f(x)=f(-x) Y se sabe que es impar
Y como se sabe numéricamente que no tiene pariedad	Porque no va a dar ni como par ni como impar