Datos sin agrupar	Los datos aparecen según se fueron registrando y no se encuentran contabilizados ni clasificados. Se trabaja con DSA cuando hay muy pocos datos.
Medidas descriptivas objetivo	Caracterizar una distribución por medio de un número reducido de medidas numéricas.
Medidas decriptivas	Estas medidas están rigurosamente definidas y dan información resumida del conjunto de datos y una idea del commportamiento global de la p o muestra.
Medidas de tendencia central	-Media aritmética -Mediana -Moda
Medidas de posición	-Cuartiles -Quintiles -Deciles -Percentiles
Medidas de dispersión	-Rango -Varianza -Desviación Típica -Desviación intercuartil -Coeficiente de variación
Medidas de forma	-Coeficiente de Fisher -Coeficiente de Pearson -Curtosis
Medidas de tendencia central	Tienden a estar en el centro de la distribución de datos. Caracterizan el centro de la distribución, esto es: al rededor de qué valor se agrupan los datos.
Medidas de posición	Sus valores fraccionan al conjunto ordenadado de unidades elementales según el valor de la variable.
Medidas de dispersión	Aquellas que describen cuán dispersos están los datos. Se pueden medir respecto a la alguna medida de tendencia central o no.
Medidas de forma	Describen la forma de la distribución de datos. Permiten comprobar si una distribución de frecuencia presenta características especiales como simetría, asimetría o nivel de apuntamiento que la puedan clasificar en un tipo particular de distribución.
Asimetría	Con estas formas se trata de establecer si una distribución de datos es asimétrica o no, y en segundo caso el grado de asimetría.
Curtosis	Mide la agudeza (elevación o achatamiento) de una distribución de datos comparada con la distribución normal.
Media Ventajas	-Fácil manejo algebráico y posee propiedades que la hacen aptas para la construcción de otras medidas descriptivas. -Utiliza todos los datos. -Se expresa en la misma unidad que la variable en estudio. -Es una medida familiar para la mayoría. -Es un valor único.
Media desventajas	-Se ve afectada por los valores extremos. -Solo se usa para variables cuantitativas.
Mediana	Valor de la variable en estudio que divide al conjunto de datos observados en dos mitades iguales. El 50% será menor o igual a este valor, y el otro 50% mayor o igual.
Cálculo de la mediana
Mediana	Ventajas: -El cálculo es fácil y rápido. -No se ve afectada por valores atípicos, es una medida robusta. Desventajas: -No intervienen todos los datos. -Es necesario ordenar los datos.
Moda	Aquel valor de la variable en estudio que se presenta con mayor frecuencia.
Moda	Ventajas: -Fácil de interpretar. -No se ve afectada por valores atípicos.-Para datos cuantitativos y cualitativos. Desventajas: -No intervienen todos los datos.-No siempre existe.-Si tiene + de una es difícil de interpretar.
Medidas de posición. Cuantiles	Son valores de la variable en estudio que dividen al conjunto ordenado de datos observados en fracciones de tal manera que deja un porcentaje k % de unidades elementales por debajo de ese valor y un (100-k) % por encima del mismo.
Cálculo cuantiles
Medidas de dispersión	Son aquellos valores numéricos que nos dan info sobre cuán esparcidos o concentrados están los datos.
Medidas de dispersión absolutas y relativa	Absolutas: Rango, Varianza, Desviación típica y Desviación intercuartílica. Relativa: Coeficiente de variación.
Rango	Es el valor máximo de la variable menos el valor mínimo. Rango=Xn-X1
Rango	Ventajas: -Fácil de calcular. -Útil cuando se quiere conocer la extensión de variaciones extremas. Desventajas: -Solo intervienen 2 datos. -Influenciada por valores extremos, resultando una medida inestable afectada por el tamaño de muestra.
Rango intercuartílico o Desviación intercuartílica	Indica la amplitud del 50% central de la distribución de datos ordenados. RI= Q3 - Q1
Rango Intercuartílico	Ventaja: -No se ve influenciada por valores atípicos. Desventaja: No utiliza todos los datos.
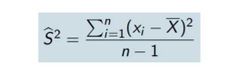
Varianza	Es el promedio de los cuadrados de las desviaciones de los valores respecto a la media aritmética.
Varianza	Ventaja: -En su cálculo intervienen todos los datos. Desventaja: -Se pierde la unidad de medida original.
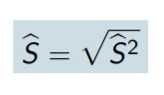
Desviación típica	Para solucionar el problema de que la unidad de medida de la Varianza queda al cuadrado, calculamos la raíz cuadrada, así surge el concepto de la Desviación Típica.
Desviación típica	Ventajas: -Intervienen todos los datos. -Expresada en las mismas unidades que la variable en estudio. Desventajas: -No tiene.
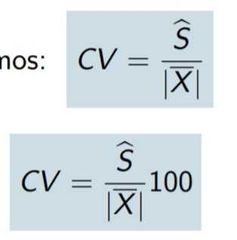
Coeficiente de variación	Resulta muy útil para comparar comportamiento de poblaciones distintas, a menor coeficiente de variación, menor dispersión en torno a la media.
Coeficiente de asimetría	Grado de simetría de una distribución respecto a una medida de tendencia central (que generalmente es la media aritmética).
Coeficiente de variación	La distribución puede ser:
Coeficientes de asimetría
Coeficiente de Fisher
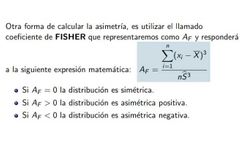
Curtosis	Se aplica a distribuciones unimodales simétricas o ligeramente asimétricas, ya que representa la elevación o achatamiento de una distribución comparada con la distribución normal
Curtosis