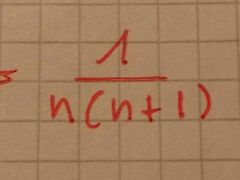
a que seria igual esta forma?
cual es la formula para hallar la suma aritmetica de una sucesion
cual es la formula para hallar el ultimo termino de una sucesion aritmetica ?
formula para hallar la sumatoria de kos terminos de una sucesion geometrica
formula para hallar el ultimo numero de una sucesion geometrica
was ist eine nullfolge ?	ist eine folge von reelen zahlen die gegen 0 konvergiert oder sich annähert... limit = 0
cual es la formula general de grenzwert
cual es la sumatoria de esta forma	1
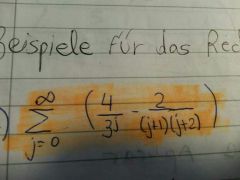
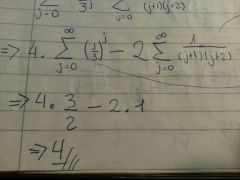
como se resuelve este problema	1 .numeradores salen de el simbolo sumatoria. 2. se resuelve lo q esta en el simbolo sumatoria ( formulas ). 3. se opera.
si el valor absoluto de q es menor que 1 en la imagen .. que se cumplira o a q sera igual la sumatoria?	que la sumatoria de ese q elevado a la j sera 1/ 1-q
a q sera igual la sumatoria de	e y vale :2.7182
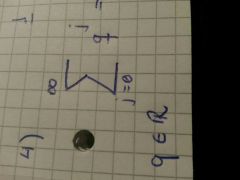
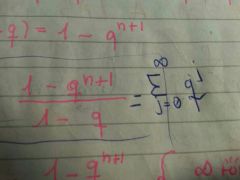
como se llama esta sumatoria y cual es su solucion	se llama geometrische Reihe y su solucion es y tiene q comenzar desde 0 ... si q es menor que 1 entonces el valor de la sumatoria sera un aproximado a 1/1-q.. si la sumatoria comienza desde 1 sera.. ( 1/1-q ) -1
que significa que una serie es divergent?	es q la serie es infinita
cual es el limite de la sumatoria de geometrische reihe de q ?	.si el valor absoluto de q es igual o mayor que 1 sera divergent. .si el valor absoluto de q es menor que 1 sera 1/1-q su limite
cual es el nombre de esta reihe	harmonische Reihe
dar sus limites
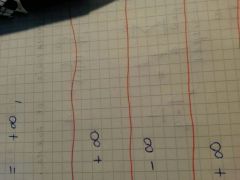
dsr sus limites
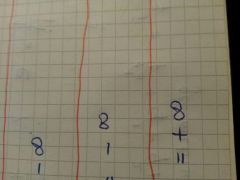
diferrentiales. dar sus difernciales
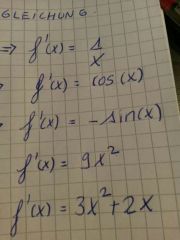
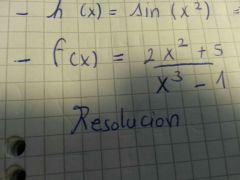
hallar la diferencial de f(x)
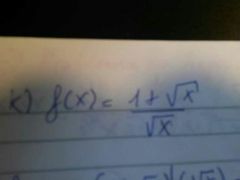
hallar la diferentiall de
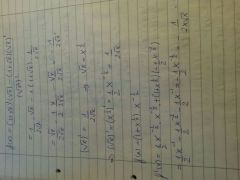
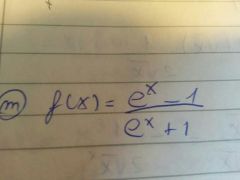
hallar la diferential de
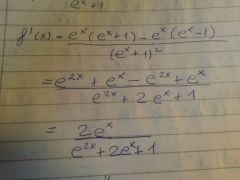
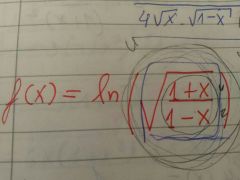
hallar
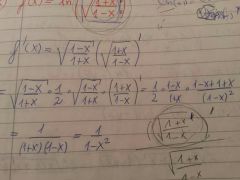
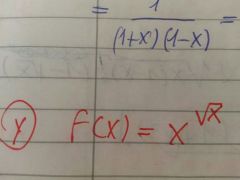
hallar
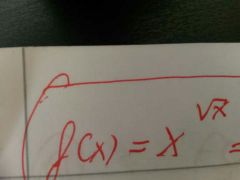
q propiedad es esta ?
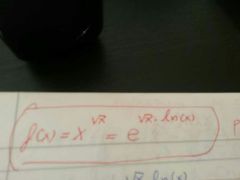
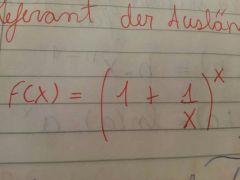
hallar
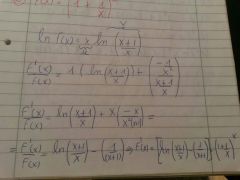
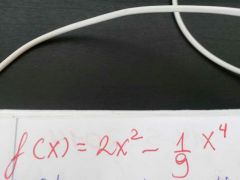
hallar
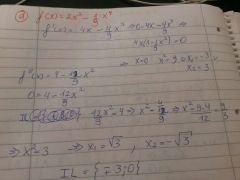
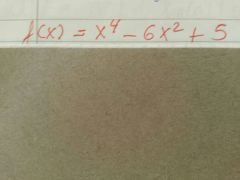
hallar
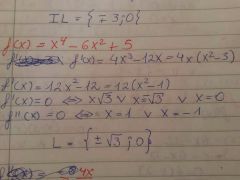
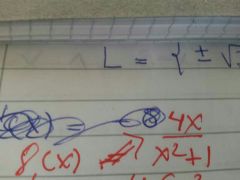
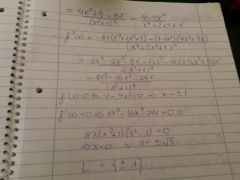
hallar	hay mass...	mass
a que es igual esta forma
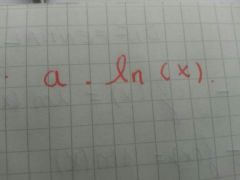
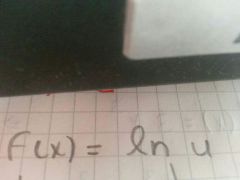
a q es igual la diferencial del logaritmo neperiano
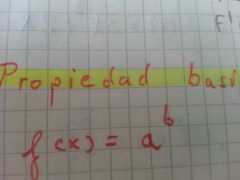
propiedas basica diferencial