Axioma 1	existen infinitas rectas infinitos planos e infinitos puntos en el espacio. en el plano existen infinitos puntos e infinitas rectas	infinitos
axioma 2	por un punto del plano pasan infinitas rectas. el punto pertenece a las rectas y las rectas están contenidas en el plano	haz de recta
axioma 3	dos puntos cualesquiera del plano determinan una única recta. los puntos pertenecen a la recta y la recta está contenida en el plano	dos puntos
axioma 4	existen infinitos puntos que pertenecen a una recta y existen infinitos puntos que no pertenecen a ella	pertenecen Y no pertenecen
axioma 5	los puntos de cualquier recta R están ordenados según dos órdenes opuestos	orden
axioma 6	dados dos puntos distintos de una recta existen por lo menos un punto de la misma entre ambos	punto intermedio
axioma 7	Tres puntos no alineados determinan un único plano al que pertenecen	Tres puntos
axioma 8	dada una recta existen infinitos planos en los cuales está contenida	recta contenida
axioma 9	por un punto exterior a una recta pasa una sola recta paralela a ella. observación: la condición de existencia es demostrable. la de unicidad es axiomática	paralela
axioma 10	dado un punto cualquiera de un plano y una recta cualquiera contenida en este plano, por el punto pasa una única recta perpendicular a la primera.	perpendicular
axioma	son enunciados o afirmaciones que no se demuestran y que se consideran válidas	afirmaciones
teorías axiomáticas	se basan en razonamientos deductivos (gral a lo particular) construidos a partir de un conjunto de conceptos primitivos entes que no se definen pero que uno entiende su significado	primitivos
semirrecta	sea una recta R y un punto o perteneciente a la recta R y un orden para la recta R. El punto o determina dos conjuntos de puntos denominados semirrectas opuestas entre sí.	conjuntos
segmento	dada la recta R y los puntos a y b pertenecientes a ella y no coincidentes. Se define como el segmento a a la intersección de la semirrecta de origen b a la que pertenece a y la semirrecta de origen a a la que pertenece b.	intersección
semiplano	dado el plano Alfa y una recta R cualquiera contenida en él. La misma determina en el plano dos subconjuntos de puntos denominados semiplano. La recta R se denomina borde de los semiplanos.	subconjuntos
conjunto convexo	un conjunto de puntos es convexo si y sólo si al considerar dos puntos cualesquiera pertenecientes Al conjunto. el segmento determinado por ellos está íntegramente contenido en el conjunto.	segmento
conjunto de puntos cóncavo	un conjunto de puntos es cóncavo si y sólo si dos puntos pertenecientes Al conjunto determinan un segmento que no está contenido en el conjunto	segmento no contenido
ángulo convexo	Sean las semirrectas oa y Ob contenidas en las rectas R&T que no son coincidentes y se intersectan en el punto o. Se define como ángulo convexo (boa) a la intersección de los dos semiplanos	intersección
ángulos Opuestos por el vértice	dos ángulos se dicen Opuestos por el vértice si y sólo si los lados de uno de ellos son semirrectas opuestas a los lados del otro	los lados
ángulos adyacentes	dos ángulos son adyacentes si y sólo si tienen un lado en común y los otros dos lados Son semirrectas opuestas	un lado
ángulos consecutivos	dos ángulos son consecutivos si y sólo si la intersección de ambos da como resultado 1 de sus lados	la intersección
teorema de los ángulos Opuestos por el vértice	los ángulos Opuestos por el vértice son congruentes. se demuestran con el ángulo llano	congruentes
rectas perpendiculares	Dos rectas son perpendiculares sí solo si se intersectan en un ángulo recto	recto
distancia entre un punto y una recta	la distancia entre un punto y una recta. es igual a la longitud del segmento perpendicular trazado desde el punto a la recta. la longitud es el valor absoluto del segmento.	segmento
rectas paralelas	dos rectas de un mismo plano son paralelas si no tienen puntos en común. las rectas pertenecen al plano y la intersección es igual al conjunto vacío.	puntos en común
teorema 1 de rectas	si dos rectas de un plano son perpendiculares a una tercera recta entonces son paralelas entre sí. Se demuestra en un solo sentido por el método del absurdo negando que sean paralelas.	tercera recta
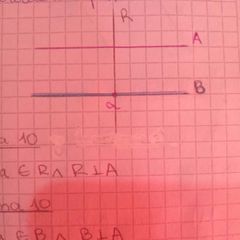
teorema 2 condición de existencia del axioma de euclides	dado un punto exterior a una recta siempre existe una segunda recta a la cual el punto pertenece Y es paralela a la primera. se demuestra en un solo sentido por el método directo aplicando el axioma 10 para trazar la recta B y la recta R y como R es perpendicular A y también a B entonces A es paralela a B
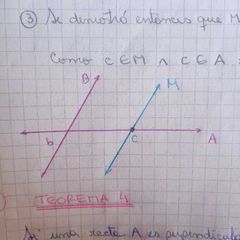
teorema 3 de rectas	si una recta A intersecta a otra recta B en un punto, entonces interceptará a toda otra recta paralela a la recta B. aquí hay que poner una recta M que es paralela a B y qué tiene que intersectar a la recta A en un punto c, que es exterior a B. hay que demostrar que c pertenece a las rectas A y M (axioma 9), Entonces es su punto de intersección.
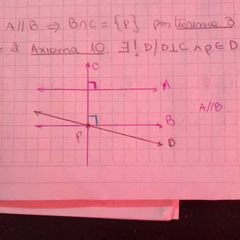
teorema 4 rectas	si una recta A es perpendicular a otra recta C. Entonces C es perpendicular a toda recta B paralela a la recta A. Se demuestra por el método del absurdo suponiendo que C no es paralela a B. por el teorema 3 podemos decir que las rectas B y C tienen un punto en común P y aplicando el axioma 10 obtenemos una recta perpendicular D distinta a B. como hay dos perpendiculares podemos decir qué la recta A es paralela a la recta D y cómo nos encontramos con dos rectas paralelas que pasan por el mismo punto. Llegamos al absurdo.
ángulos formados por dos rectas cortadas por una transversal	una recta que corta dos o más rectas de su plano en puntos no coincidentes se llama transversal. sean R y S dos rectas no coincidentes de un plano pi cortadas respectivamente en los puntos a y b por una transversal T quedan determinados ocho ángulos.	no coincidentes
ángulos correspondientes	dos ángulos no adyacentes son correspondientes si y sólo si están contenidos en el mismo semi plano con respecto a la transversal uno es interno y el otro es externo	el que le corresponde
ángulos alternos	dos ángulos no adyacentes son alternos si y sólo si están contenidos en distintos semiplanos con respecto a la transversal ambos interiores o ambos exteriores
ángulos conjugados	dos ángulos no adyacentes son conjugados si y sólo si están contenidos en el mismo semiplano respecto de la transversal
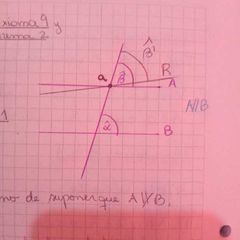
teorema 5 de ángulos correspondientes	sean Alfa y Beta dos ángulos correspondientes formados entre paralelas las rectas son paralelas si y sólo si los ángulos son iguales tiene demostraciones en dos sentidos primero demostramos que los ángulos son iguales aplicando una recta perpendicular y sumando los ángulos interiores de los triángulos en segundo lugar usamos el método del absurdo para decir que las rectas no son paralelas y buscamos una recta r que parece paralela a b y forma un ángulo beta prima que parece ser igual a Beta y produce una contracción
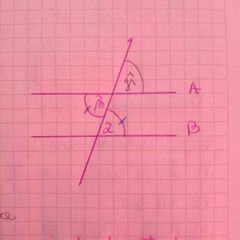
teorema 6 ángulos alternos	sean Alfa y Beta ángulos alternos formados entre paralelas las rectas son paralelas si y sólo si los ángulos son iguales se demuestra en dos sentidos primero se demuestra qué los ángulos son iguales usando un ángulo auxiliar correspondiente que también es opuesto por el vértice en segundo lugar se prueba que las rectas son paralelas diciendo que los ángulos son correspondientes
teorema 7 ángulos conjugados	sean Alfa y Beta ángulos conjugados formados entre paralelas. las rectas son paralelas si y sólo si la suma de los ángulos es 180°. se demuestra en los dos sentidos primero por el método directo usando un ángulo auxiliar Qué es correspondiente y suma 180° por ser adyacente en segundo lugar se prueba que las rectas son paralelas demostrando que estos ángulos correspondientes son iguales igualando las sumas
triángulo	si en tres puntos no alineados a b c pertenecientes a un mismo plano pi se define Cómo triángulo a la intersección de los tres ángulos. los ángulos tienen cuatro elementos ángulos adyacentes y se clasifican en tres tipos según sus lados, los equiláteros son isósceles y los conjuntos no forman una partición porque son disjuntos también se clasifican por sus ángulos
mediatriz de un triángulo	se define como mediatriz de un triángulo al segmento que siendo perpendicular a uno de sus lados lo divide en dos partes congruentes CIRCUNCENTRO en los triángulos rectángulos se encuentra en el centro de la hipotenusa y en los obtusángulos se encuentra en el exterior siempre Tres puntos no alineados determinan una única circunferencia	perpendicular lado medio
bisectriz de un triángulo	se define como bisectriz de un triángulo el segmento de la bisectriz del ángulo interior contenido en el triángulo que divide el ángulo en dos partes congruentes y terminan en correspondiente lado opuesto INCENTRO equidista de los lados porque es igual que el radio	segmento
mediana de un triángulo	se define como mediana de un triángulo el segmento trazado desde el vértice a la mitad del lado opuesto GRAVICENTRO tiene tres partes en este punto la figura tiene equilibrio porque las masas se distribuyen uniformemente el gravicentro siempre se encuentra en el interior de un triángulo
altura de un triángulo	se define como altura de un triángulo el segmento trazado desde el vértice perpendicular al lado opuesto o a la prolongación del lado opuesto ORTOCENTRO en el triángulo rectángulo coincide con el vértice del ángulo recto y en el obtusángulo puede estar en el exterior
recta de Euler	o g y c en equilátero coinciden, y hay una relación en el triángulo isósceles también aparece i y la recta de Euler es su eje de simetría
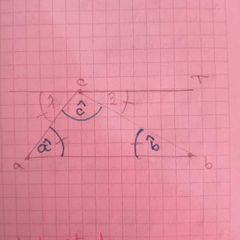
teorema de los ángulos interiores de un triángulo	en todo triángulo la suma de las amplitudes de los ángulos interiores mide 180° esto se demuestra con una recta paralela a la base que forma un ángulo llano con ángulos alternos
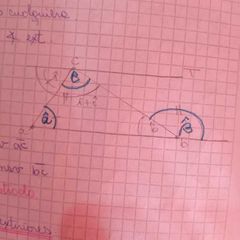
teorema del ángulo exterior	en todo triángulo la medida de un ángulo exterior cualquiera es igual a la suma de las medidas de los ángulos interiores no adyacentes esto se demuestra con una recta paralela a la base dónde se suma el ángulo de arriba con una alterno y eso es igual al ángulo externo
teorema de Pitágoras	en todo triángulo rectángulo el cuadrado de la medida de la hipotenusa es igual a la suma del cuadrado de las medidas de los catetos demostración geométrica y formal
recíproco del teorema de Pitágoras	sea ABC un triángulo cualquiera no equilátero y a el mayor de los tres lados y el cuadrado de la medida de la hipotenusa es igual a la suma del cuadrado de la medida de los catetos Entonces el Triángulo ABC es rectángulo en a se demuestra con el teorema del coseno
teorema 1 de triángulos	si un triángulo tiene dos lados congruentes Entonces los ángulos Opuestos a esos lados también son congruentes se demuestra por el método directo trazando la bisectriz del ángulo Superior y doblamos la figura por esta
teorema 2 de triángulos y reciproco	si un triángulo tiene dos lados desiguales entonces a mayor lado se opone mayor ángulo. se demuestra metiendo un triángulo isósceles
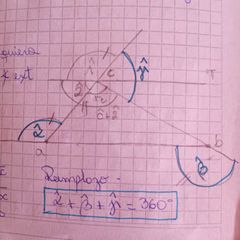
teorema de los ángulos exteriores	en todo triángulo la suma de las medidas de los tres ángulos exteriores es igual a 360 grados esto se demuestra con una recta paralela a la base y un ángulo de un giro con partes que son correspondientes entre paralelos
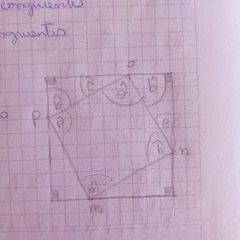
teorema de Pitágoras	en todo triángulo rectángulo el cuadrado de la medida de la hipotenusa es igual a la suma del cuadrado de la medida de los catetos esto tiene una demostración geométrica que al restar los cuatro triángulos las áreas que quedan son iguales y tiene una demostración formal donde se prueba que los lados del cuadrado son iguales por ser hipotenusa y los ángulos tiene 90 grados porque forman un ángulo llano y son ángulos interiores de un triángulo
recíproco del teorema de Pitágoras	te ABC un triángulo cualquiera no equilátero y a el mayor de los tres lados y el cuadrado de la medida de la hipotenusa es igual a la suma del cuadrado de las medidas de los catetos Entonces el Triángulo ABC es rectángulo en A se demuestra con el teorema del coseno: un lado cualquiera del triángulo cualquiera es igual a la suma de los cuadrados de los otros dos menos el doble producto de ellos por el coseno del ángulo que forman esos lados por hipótesis la parte del coseno vale 0 entonces el ángulo mide 90
teorema 1 de los triángulos	si un triángulo tiene dos LADOS congruentes Entonces los ángulos Opuestos a esos lados también son congruentes si un triángulo tiene dos ANGULOS congruentes Entonces los lados Opuestos a estos ángulos también son congruentes esto se demuestra doblando la figura sobre su bisectriz Y entonces coinciden los lados y coinciden los ángulos y podemos ver que los ángulos son iguales el recíproco se demuestra por el absurdo usando el teorema 2 y suponiendo que un ángulo Es mayor que el otro
teorema 2 de los triángulos y reciproco	si un triángulo tiene dos LADOS desiguales entonces a mayor lado se opone mayor ángulo si un triángulo tiene dos ANGULOS desiguales entonces a mayor ángulo se opone mayor lado se demuestra dibujando un triángulo isósceles dentro del rectángulo el recíproco se demuestra por el absurdo suponiendo que un lado es menor o igual al otro aplicamos teorema 1 y teorema 2
teorema 3 de triángulos	el triángulo equilátero es equiángulo se demuestra por teorema 1 qué lados iguales y ángulos iguales después se suma todos a 180 y Al despejar me queda que cada ángulo mide 60
teorema 4 de triángulos	en todo triángulo un lado es menor que la suma de los otros dos y mayor que su diferencia falta la demostración
congruencia de triángulos	dos triángulos son congruentes si y sólo si tienen respectivamente congruentes sus tres lados y sus tres ángulos observaciones 1. desde el punto de vista de la homotecia dos triángulos son congruentes si y sólo si mediante movimientos se pueden superponer de manera que coincidan todos sus puntos 2. desde el punto de vista matemático se establece una correspondencia biunivoca a cada punto del primero le corresponde uno y sólo un punto del segundo y viceversa. 3. en dos triángulos congruentes al establecer una correspondencia entre los vértices también queda establecida la correspondencia entre los lados 4. la correspondencia es simétrica reflexiva y transitiva.
criterio LLL	sí dos triángulos tienen sus lados respectivamente congruentes entonces son congruentes
criterio LAL	sí dos triángulos tienen dos lados respectivamente congruentes y los ángulos comprendidos congruentes entonces son congruentes
criterio LLA	sí dos triángulos tienen dos pares de lados respectivamente congruentes y el ángulo opuesto al mayor de ellos es congruentes entonces son congruentes observación: en triángulos congruentes a lados congruentes se oponen ángulos congruentes y recíprocamente
criterio ALA	sí dos triángulos tienen un solo par de lados respectivamente congruentes y los ángulos adyacentes a ellos congruentes Entonces son congruentes