definición de derivada	teniendo una función f definida en un intervalo abierto, la función tiene derivada en un punto (a) si existe el limite del cociente incremental y que sea número real
cociente incremental	◇y f(x) - f(a) incremento función ◇x x-a incremento de variable
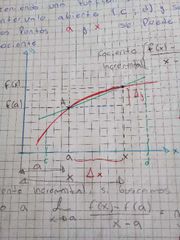
grafico para sacar cociente incremental	Cateto opuesto cateto adyacente
interpretacion geometrica de la derivada	geometricamente, la derivada de uma función en un punto es LA PENDIENTE DE LA RECTA TANGENTE
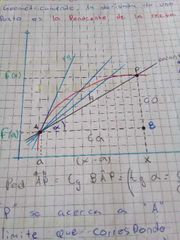
grafico de la interpretación geométrica de la derivada	la misma del cociente incremental sin el interalo abierto
teniendo una función derivable, para sacar su tangente...	teniendo un punto que ya conocemos (a, f(a)) usamos la ecuación de la recta por un punto
recta normal	es perpendicular a la recta tangente asi que buscamos el inverso multiplicativo de la pendiente de la recta tangente cambiada de signo
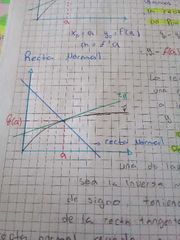
recta normal y tangente Grafia	f(x) derivable
cuando una función es derivable	cuando existe el limite del incremento de y y el incremento de x (cociente incremental) para ese punto y este da como resultado un número real
continuidad de una función	una función derivable asegura que esta función es continua, pero que sea continua no asegura que sea derivable
continua pero no derivable	una función como \|x\| es continua em x=0 pero al aplicar la definición no es derivable
por que \|x\| no es derivable si es continua?	porque presenta un pico y se dice que para que una función sea continua en toda la función debe ser sin picos/esquinas
dx	es una variable independiente a la que se le puede dar valoresreales
dy	es una variable dependiente ya que es igual a f'(x). dx
dy=f'(×).dx	si pasamos dx dividiendo me queda el cociente diferencial
◇y	◇y + dx = esto lo reemplazo en f(x) f(x) -f(1) = incremento de y
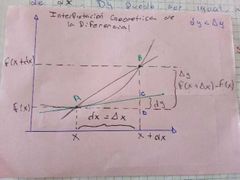
interpretación geométrica de la diferencial	igual a la de interpretación geométrica de la derivada dada vuelta
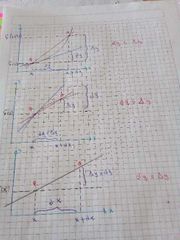
dy siempre da un solo resultado?	puede ser menor al incremento de y como el gráfico principal, mayor la tangente arriba de la grafica o igual donde todas cruzan igual
tasa razón promedio	de cambio de y por unidad de cambio de x cuando pasa de A a X. se saca con el cociente incremental
tasa razón instantánea	punto a punto de cambio de y por unidad de cambio de x en a siempre y cuando exista limite para ese punto y que de un numero real se saca El limite del cociente incremental = F'(×)
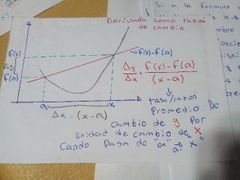
Derivada como razón de cambio	sacamos la razón de cambio promedio/ instantánea

Descubre

Crear Tarjetas

Acerca de Nosotros

Explore Tarjetas

Comparta este Set de Tarjetas de Aprendizaje

Unida 4

Cómo estudiar sus tarjetas

Rango de Cartas a estudiar

21 Cartas en este set