	Las cadenas binarias que no contienen la subcadena 01
	\|\| F \|\| = 0
Sea l la longitud de una computación para una cadena w en un AFND. Entonces:	l puede ser mayor que \|w\|
Dado el alfabeto Σ = {0,1} ¿cuántos estados tiene el AF mínimo que reconoce el lenguaje L = {01, 10}?	2
El lenguaje generado por una gramática en Forma Normal de Chosmky	nunca contiene la cadena vacía
¿Cuántos lenguajes hay sobre un alfabeto dado de modo que no haya cadenas sobre dicho alfabeto que sean distinguibles respecto a ese lenguaje?	Dos
En un AFD, la función transición δ se define como	δ: K x Σ -> K
Dado un alfabeto Σ y un lenguaje L contenido o igual en Σ*, con \|\|L\|\| = 3 y sin la cadena vacía, y sea A el AF que reconoce L con el menor número de estados posibles \|\|K\|\|. ¿Valor de K?	\|\|K\|\| = 2
Dado un lenguaje regular que contiene la cadena vacía	Para cualquier AFD que lo reconozca, su estado inicial es siempre final
Dado un AFND que reconoce un lenguaje L, ¿cuántas computaciones de aceptación (n) puede tener una cadena que pertenece a L?	n>= 1
¿Verdadero o falso? Toda gramática que es recursiva por la derecha e izquierda a la vez es ambigua	Falso
¿Verdadero o falso? Toda gramática que es recursiva por la derecha e izquierda a la vez no es regular	Verdadero
¿Verdadero o falso? Toda gramática que es recursiva por la derecha e izquierda a la vez genera un lenguaje inherentemente ambiguo	Falso
¿Una gramática propia puede generar el lenguaje vacío?	No
¿Una gramática propia puede ser ambigua?	Sí
¿Una gramática propia puede ser recursiva?	Sí

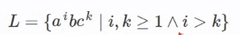
Sea L un lenguaje regular y M el AFD mínimo que lo reconoce. Entonces:	Para algunos lenguajes regulares puede haber AFNDs que los reconocen con menos estados que sus respectivos AFDs mínimos
(q0, baababaaa) \|- (q1, ababaaa) \|- (q3, babaaa) es una computación...	es una computación de un posible AFND
L = Ø ¿Cumple la CBR? ¿Y la CBCL?	Cumple la CBR y la CBCL
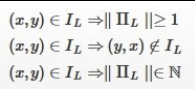
Marca la afirmación verdadera	La primera es la verdadera
El teorema de Myhill-Nerode se suele utilizar para demostrar que un lenguaje	no es regular
Si L₁ y L₂ son lenguajes de contexto libre, entonces también lo es:	(L₁L₂∪L₁)
Si GCL es ambigua si el lenguaje que genera	es inherentemente ambiguo
Sea ΠL la partición que permite que un lenguaje L verifique el teorema de Myhill-Nerode, y sea F el conjunto de estados finales del AFD que reconoce L. Entonces se cumple que:	\|\|F\|\| ≤ \|\|ΠL\|\|
Los autómatas con pila no deterministas reconocen lenguajes de tipo...	De tipo 2
¿Los AFND pueden alcanzar estados de bloqueo?	Sí
Una gramática propia no puede	no puede generar el lenguaje vacío
Sea M un APND:	SI ninguna computación de M altera el contenido de la pila entonces L(M) ∈ L.3
En la condición de bombeo regular, siendo x = uvw, se cumple que:	\|v\| > 0
Una GCL es ambigua si:	existe una cadena del lenguaje generado por la gramática que es producto de más de un árbol de derivación.
Una gramática es propia si	no es recursiva izquierda y no tiene símbolos inútiles
Un lenguaje inherentemente ambiguia:	es aquel que no puede ser generado por una gramática no ambigua.
¿Toda GRI esta en FNG?	Sí
¿Una gramática de tipo tres siempre está en FNC?	Falso
¿Cuál es la opción correcta?	La tercera
Si un AFD = {K, Σ, δ, s, F} sin estados inaccesibles reconoce el lenguaje vacío, entonces:	\|\|F\|\| = 0
Si un lenguaje no es regular entonces siempre se verifica que:	no puede representarse con un AFD.
¿L = {0ⁿ1ⁿ} cumple la CBR?	No
L = {0ⁿ1ⁿ} es un lenguaje de tipo...	De tipo 1
¿Es L = {0ⁿ1ⁿ} un lenguaje regular?	No
Si un lenguaje cumple la condición de bombeo regular entonces	no podemos afirmar que es regular
Sea el lenguaje L = {ε}. ¿Cuántos AFND aceptan dicho lenguaje?	Infinitos
Dado un AFND que reconoce un lenguaje L, ¿Cuántas computaciones de aceptación (n) puede tener una cadena que pertenece a L?	n ≥ 1
¿Cuántos lenguajes hay sobre un alfabeto dado de modo que no haya cadenas sobre dicho alfabeto que sean distinguibles respecto a ese lenguaje?	Dos
Sea L la longitud de una computación para una cadena w en un AFND. Entonces:	L ≤ \|w\|
Sea L un lenguaje regular y M el AFD mínimo que lo reconoce. Entonces:	Para algunos lenguajes regulares puede haber AFNDs que lo reconocen con menos estados que sus respectivos AFDs mínimos.
Cuando, al menos, una cadena de un lenguaje generado por una GCL es el producto de más de un árbol de derivación,	La gramática es ambigua
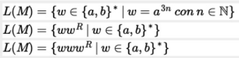
Si M = ( {s,f}, {a,b}, {a,b}, {((s, aa, ε), (s,b)), ((s, εa, ε), (f,ε)), ((f, a, b), (f,ε))}, s, {f} ) entonces (elige opción)	La primera opción
Los lenguajes de contexto libre son cerrados para las operaciones de:	unión, concatenación y estrella de Kleene
El lenguaje generado por una gramatica en Forma Normal de Chomsky:	nunca contiene la cadena vacía
Si una GCL es recursiva por la izquierda, entonces	existe una GCL equivalente que no es recursiva por la izquierda
Dado el AFND M, ¿qué lenguaje acepta?	(ab)*
Dado un lenguaje de contexto libre L, representable mediante una grámatica en forma normal de chomsky (FNC), su lenguaje complementario Lc:	En ningún caso puede ser generado por una grámatica en FNC
Sea L un lenguaje. Sean x ∈L, y !∈L. Se cumple que x,y son distinguibles con respecto a L. ¿Verdadero o falso?	Verdadero SIEMPRE
Dado el lenguaje L ={ x^n y^n : n >= 0}, el lema del bombeo para dos lenguajes regulares permite demostrar que:	No es posible construir un automata finito que reconozca L
Si L es un lenguaje de contexto libre, entonces no cumple el lema de bombeo para lenguajes regulares. ¿Verdadero o falso?	Falso
Si un simbolo no terminal de una gramática G es terminable, entonces se cumple siempre que L(G) ≠ Ø ¿Verdadero o falso?	Falso
Si (q,u,w) es una configuración de bloqueo de M, siendo M un APND, entonces w !∈ L(M) ¿Verdadero o falso?	Falso
¿Toda GCL tiene al menos un símbolo útil?	No
¿Toda GCL tiene al menos un símbolo accesible?	Sí
¿Una gramática puede tener un símbolo que sea accesible, terminable e inútil?	Sí
La relación de indistinguibilidad es una relación...	Es una relación binaria sobre Σ∗ .
El teorema de Myhill-Nerode se suele utilizar para demostrar que un lenguaje	no es regular
Los autómatas con pila no deterministas	representan lenguajes de tipo 2
El conjunto de configuraciones iniciales de un AFD definido por (K,Σ, δ,s,F):	es infinito
Un AFND transita en función de	un estado y un prefijo de la cadena
En un diagrama de estados de un AFND	una etiqueta representa la subcadena consumida
Dados L ⊆ Σ∗ y x,y ∈ Σ∗. Si (xz ∈ L ∧ yz ∈ L) ∀z ∈ Σ∗ entonces:	x e y son indistinguibles
Si M es un AFDM entonces	todos los AFD equivalentes tienen mayor o igual número de estados que M
¿Un AFDM puede tener estados inaccesibles?	No, no puede tener estados inaccesibles
¿Un AFDM tiene menos estados que cualquier AFND equivalente?	No
¿Un AFDM puede tener configuraciones de bloqueo?	No
Si dado un lenguaje L⊆Σ∗, todas sus cadenas son indistinguibles entre sí, entonces	L=Σ∗ ó L=∅
Si L cumple la CBCL entonces	Es un lenguaje de tipo 2
¿Toda GRI está en FNG?	Sí
¿Una gramática de tipo tres siempre está en FNC?	No
¿Una gramática recursiva por la izquierda puede estar en FNG?	No
L (AFD) =	L (AFND)
El conjunto de configuraciones terminales de un AFD definido por (K,Σ, δ,s,F) :	tiene el mismo cardinal que K
Si x, y ∈ Σ∗ y son indistinguibles respecto a L, entonces ∃ z ∈ Σ∗ tal que	(xz ∈ L ∧ yz ∈ L) ∨ (xz ∉ L ∧ yz ∉ L)
Un APND, con conjunto de estados finales F, acepta una cadena w si y sólo si	ⱻ q ϵ F / ( s, w, e) ->* ( q, e, e)
L(APND) =	L.2
En un AFD: ¿puede haber menos computaciones completas que cadenas aceptadas?	No
En un AFD: ¿puede haber más computaciones completas que cadenas aceptadas?	Sí
Una GCL es ambigua sii	ⱻw ϵ L(G) / w es producto de más de un árbol de derivación
Si un AFD acepta un lenguaje finito L entonces	el cardinal del lenguaje es menor que el número de estados del AFD
Una gramática es propia si	no es recursiva izquierda y no tiene símbolos inútiles
En un APND una configuración	es una terna perteneciente a K×Σ∗×Γ∗
Si M = ( {s,f}, {a,b}, {a,b}, {(( s, aa, ϵ ), (s, b)), (( s, ϵ, ϵ ), (f, ϵ)), (( f, a, b), (f,ϵ ))}, s, {f}) entonces	L(M)={w∈{a,b}∗\|w=a3nconn∈N}
Sea M un APND:	Si ninguna computación de M altera el contenido de la pila entonces L(M) ∈ L.3 .