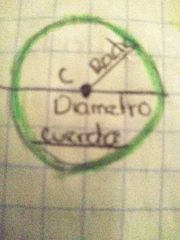
Qué es la circunferencia	circunferencia es el conjunto de todos los puntos del plano que equidistan en un mismo punto llamado centro este punto no pertenece a la circunferencia	el contorno
radio	es un segmento que une el centro de la circunferencia con cualquier punto de ella y se identifica con la letra r la medida del radio es constante
cuerda	es el segmento que une dos puntos de la circunferencia y que tiene diferentes medidas	.
diámetro	es la cuerda que pasa por el centro de la circunferencia el diámetro de la cuerda de mayor medida
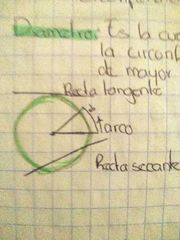
recta tangente	recta que intersecta en un solo punto de la circunferencia
recta secante	es la recta que intersecta dos puntos de la circunferencia	.
arco	es una parte de la circunferencia comprendida entre dos puntos de ella	.
ecuación de la circunferencia con centro en el origen	la circunferencia cuyo centro coincide con el origen y por la radio La constante r tiene por ecuación con centro en 0 0 y radio r. x²+y²=r² a esta expresión se le domina también como forma cónica de la circunferencia.	²
ecuación de la circunferencia con centro fuera del origen	la circunferencia con centro en el punto (h,k) que se ubica en cualquier lugar del plano y que tiene como radio La constante r se representa con la ecuación (x-h)²+(y-k)²=r² a esta forma se le denomina forma ordinaria de la circunferencia.
resultado obligatorio en las ecuaciones de circunferencia	x²+y²+Dx+Ey+F=0
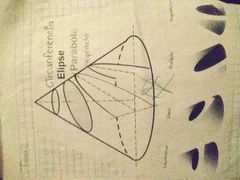
que es una cónica	la palabra cónica viene de cono se llama cónica o sección cónica a las curvas resultantes de la intersección del cono y un plato existen cuatro tipos de cónicas según el ángulo del plano que se intersecta con el cono y su base.	cono por plato
tipos de cónica	circunferencia elipse parábola hipérbola	4
circunferencia	en la intersección del cono con un plano paralelo a la base	.
elipse	intersección del cono con un plano oblicuo ala base y que no la corta en ningúnun momento	.
parábola	en la intersección de un cono con un plano paralelo a su generatriz y se cortó la base	.
hipérbola	en la intersección de un cono recto y un plato cuyo ángulo es menor al de la generatriz del cono.	.
cortés de la conica
explicación gráfica
ecuación de la circunferencia que pasa por tres puntos. pasó 1	se formó sistema de ecuaciones esto se obtiene sustituyendo cada uno de los puntos de la ecuación general de la circunferencia.
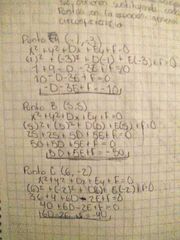
ecuación de la circunferencia que pasa por tres puntos. segundo paso	teniendo las tres ecuaciones formamos el sistema de tres ecuaciones y resolvemos con el método determinantes para obtener el valor de d e y f y así formar la ecuación general el método de determinantes consiste en cuatro reglas.
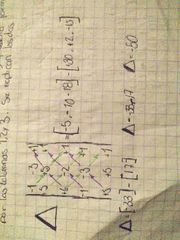
ecuación de la circunferencia que pasa por tres puntos segundo paso primer arreglo	el primer libro se llamará delta y será representado con un triángulo estará formado por las columnas 1 2 y 3 se replican Las dos últimas.
ecuación de la circunferencia que pasa por tres puntos segundo paso segundo arreglo	se le llama de estado formado por las columnas 4 2 y3 se repitan las dos primeras filas y se divide por delta
ecuación de la circunferencia que pasa por tres puntos segundo paso tercer arreglo	se llamará está formado por las columnas 1 4 y 3 y se repiten las dos primeras filas se divide por delta.
ecuación de la circunferencia que pasa por tres puntos segundo paso cuarto arreglo	se llamará f y estará formada por las columnas 1 2 y 4 y se repiten las dos primeras filas se divide por delta
ecuación de la circunferencia que pasa por tres puntos último paso	teniendo los valores de a y f formamos la ecuación general de la circunferencia sustituyendo en.

Descubre

Crear Tarjetas

Acerca de Nosotros

Explore Tarjetas

Comparta este Set de Tarjetas de Aprendizaje

Matemáticas

Cómo estudiar sus tarjetas

Rango de Cartas a estudiar

25 Cartas en este set