Identidades recíprocas o básicas	sen(x)csc(x)=1 cos(x)sec(x)=1 tan(x)cot(x)=1
Identidades de cociente	tan(x)=sen(x)/cos(x) cot(x)=cos(x)/sen(x)
Identidades pitagóricas	sen^2(x)+cos^2(x)=1 tan^2(x)+1=sec^2(x) cot^2(x)+1=csc^2(x)
Suma y resta de ángulos	sen(A+B)=senAcosB+cosAsenB sen(A-B)=senAcosB-cosAsenB cos(A+B)=cosAcosB-senAsenB cos(A-B)=cosAcosB+senAsenB tan(A+B)=tanA+tanB/1-tanAtanB tan(A-B)=tanA-tanB/1+tanAtanB
Identidades de doble ángulo	sen2A=2senAcosA cos2A=1-sen^2A 2cos^2A-1 cos^2A-sen^2A tan2A=2tanA/1-tan^2A
Identidades de la mitad del ángulo	>senA/2=√1-cosA/2 >cosA/2= √1+cosA/2 >tanA/2=√1-cosA/1+cosA= senA/1+cosA= 1-cosA/senA
Producto de senos y cosenos	>senAcosB=1/2[sen(A+B)+sen(A-B)] >cosAcosB=1/2[cos(A+B)+cos(A-B)] >senAcosB=1/2[cos(A+B)-cos(A-B)]
Fórmula de ángulos
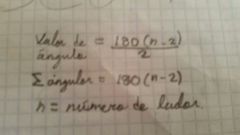
Fórmulas diagonales
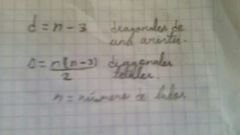
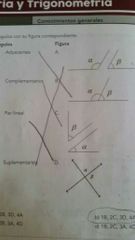
Tipos de ángulos	Complementarios: suman 90° Suplamentarios: suman 180° Conjugados: suman 360°
Ángulo inscrito
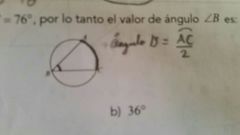
Triángulos notables
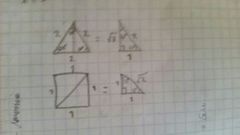
Congruencia de triángulos
Los ángulos internos de un triángulo forman=	180°
ley de senos
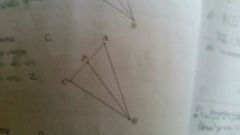
Mediana	Un vértice se une con el punto medio del lado contrario
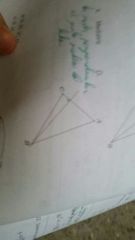
Altura	Un lado en forma perpendicular con unión a su vértice opuesto
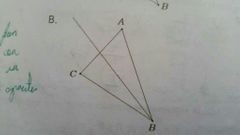
Bisectriz	Un línea parte el ángulo de un vértice a la mitad
Mediatriz	La recta perpendicular del punto medio del triángulo
teorema de pitágoras	c^2=a^2+b^2
Semejanza de triángulos
senx^2=	1/2 (1-cos2x)
cosx^2	1/2 (1+cos 2x)