definición de lógica	es la ciencia que estudia los METODOS Y PRINCIPIOS usados para distinguir los pensamientos correctos de los incorrectos	métodos y principios
razonamiento	es un tipo especial de pensamiento que a partir de ciertas AFIRMACIONES llamadas PREMISAS se derivan otras afirmaciones llamadas CONCLUSIONES	tipo especial de pensamiento
proposiciones	una proposición es una oración afirmativa, expresión de la que puede establecerse el valor de verdad: verdadero o falso	oración afirmativa
observación sobre razonamientos	los razonamientos están formados por premisas y conclusiones ambas llamadas proposiciones	están formados
observaciones sobre proposiciones	la determinación de la verdad o falsedad de una proposición no es competencia de la lógica	la verdad
los símbolos de la lógica	las proposiciones serán demostradas con letras minúsculas del alfabeto	letra
proposiciones equivalentes	dos proposiciones son equivalentes si tienen el mismo valor de verdad obs: son proposiciones diferentes pero son equivalentes, toda vez que una es verdadera la otra también y si es falsa ocurre lo mismo con la otra	p: Juan es amigo de Pedro q: Pedro tiene a Juan por amigo
proposiciones simples	una proposición se dice simple Sí sólo si No CONTIENE a otra proposición como parte Constituyente de sí misma	p: cuatro pertenece a los números pares
proposición compuesta	una proposición es compuesta si y sólo si contiene MÁS DE UNA proposición formando parte de ella	r: dos pertenece a los números pares y dos pertenece a los múltiplos de 2
operaciones proposicionales	a partir de proposiciones simples es posible GENERAR otras que pueden ser simples o compuestas es decir se puede OPERAR con proposiciones utilizando los llamados conectivos lógicos	se puede operar con conectivos lógicos
Son seis las operaciones lógicas	Negación Conjunción Disyunción Diferencia Simétrica * implicación o condicional * doble implicación o bicondicional
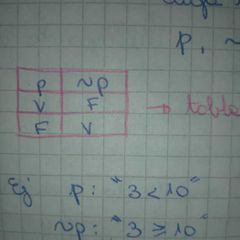
definición de negacion con tabla de verdad	negación de la proposición p es la proposición ~p, cuya tabla de verdad es:... el valor de verdad de p es contrario al valor de verdad de ~p
definición de conjunción y tabla de verdad	la conjunción de dos proposiciones P y q es la proposición (p^q) cuya tabla de verdad es:... para que la conjunción sea verdadera los dos deben ser verdaderos
definición de disyunción	la disyunción de la proposiciones P y q es la proposición (p v q) cuya tabla de verdad:... con que una sea verdadera es verdad la proposición. El signo mayor o igual representa una disyunción
definición de diferencia simétrica o disyunción excluyente	la disyunción de las proposiciones p y q es la proposición (p¥q) en sentido excluyente cuya tabla de verdad es:... una tiene que ser verdadera pero no pueden ser verdaderas las dos al mismo tiempo
definición de implicación o condicional	la implicación de la proposición P y q es la proposición P=> q cuya tde v: ... Es imposible de un verdadero llegar a un falso p y q se llaman antecedente y consecuente de la implicación Un teorema qsqd P: hipótesis, q: tesis y => son los procesos de demostración
definición de teorema	un teorema en matemáticas es una PROPIEDAD válida en un cierto dominio que debe ser demostrada hay muchos procesos de demostración posee cuatro partes:enunciado, hipótesis, tesis y demostración	propiedad
sobre el enunciado de un teorema	el enunciado ENGLOBA la hipótesis tesis y demostración simultáneamente una hipótesis son los datos, el universo donde vale la tesis la tesis es lo que quiero probar la demostración es el proceso por el cual se demuestra al tesis	engloba
definición de doble implicación o bicondicional	dados dos proposiciones p y q se define a la proposición p<=>q a la que posee la siguiente tabla de verdad:... OBs: el bicondicional también equivale a un TEOREMA cuando antecedente y consecuente son verdaderos en este caso se habla de caracterización Hay que desdoblar en dos teoremas para probarlo	caracterización
definición de tautología	una proposición COMPUESTA se denomina tautología o ley lógica si y sólo si es VERDADERA independiente de los valores de verdad de las proposiciones componentes
construcción de tabla de verdad pasó 1	siendo n el número de proposiciones simples intervinientes el número de filas de tablas de verdad es igual a 2 elevado a la n
construcción de tablas de verdad Paso 2	ordenamos en columna las proposiciones simples siguiendo el orden alfabético p q r s t
construcción de tablas de verdad pasó 3	siendo k = 1, 2, 3 o n. las proposiciones de cada columna, la alternancia de los verdaderos o falsos está dada por 2 elevado a k - 1. se puede comenzar de derecha o de izquierda
construcción de tablas de verdad pasó 4	en una fila de encabezamiento se construye por partes la proposición dada, Comenzando por las operaciones interiores y en la última columna debe estar la proposición cuya tabla de verdad queremos obtener
propiedades de las implicancias
propiedades de la implicancia
propiedades de la implicancia y negación
demostración de teorema
números reales
axiomas de los números reales axiomas de campo
intervalos
propiedades de valor absoluto
propiedades de logaritmo y raíz