- Barajar
ActivarDesactivar
- Alphabetizar
ActivarDesactivar
- Frente Primero
ActivarDesactivar
- Ambos lados
ActivarDesactivar
- Leer
ActivarDesactivar
Cómo estudiar sus tarjetas
Teclas de Derecha/Izquierda: Navegar entre tarjetas.tecla derechatecla izquierda
Teclas Arriba/Abajo: Colvea la carta entre frente y dorso.tecla abajotecla arriba
Tecla H: Muestra pista (3er lado).tecla h
Tecla N: Lea el texto en voz.tecla n
![]()
![]()
![]()
29 Cartas en este set
- Frente
- Atrás
- 3er lado (pista)
|
F(×) es primitiva de f (x )
|
Si F'(×)=f(×)
La notación es F(×)={f(×)dx |
|
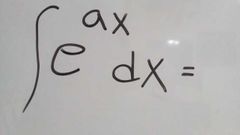
|
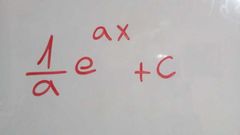
|
|
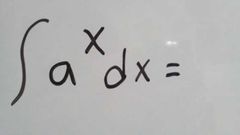
|
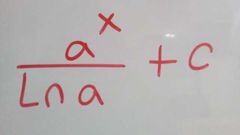
|
|
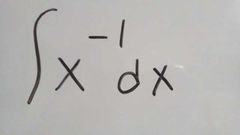
|
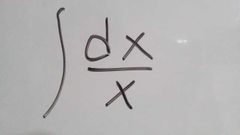
|
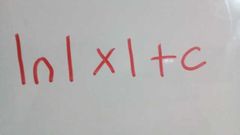
|
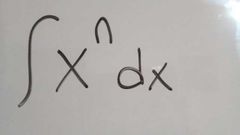
|
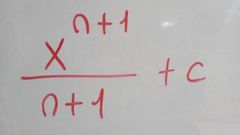
|
|
|
excedente sel consumidor
|
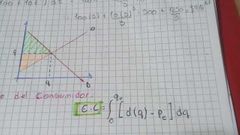
Es el area de arriba (verde)
El pe=al valor del eje y |
|
|
Excedente del productor
|

Es la parte naranja
el qe= al valor de cero hasta q |
|
|
Sacar el punto de equilibrio
|
igualamos d(q) y o(q) para que nos de q y ese es el limite que toma la integral
|
|
|
Integral de {cosxdx
|
senx
|
|
|
integral de {senxdx
|
-cosx +c
|
|
|
1
cos^2x |
tanx + C
|
|
|
Integral por parte es para cuando tenemos un producto de dos funciones
|
identificamos con ILATE
|
|
|
ILATE
|

|
|
|
Por sustitución
|

|
|
|
multiplicación por sustitución
|
lo de adentro del paréntesis derivado me da lo de afuera
|

|
|
exponencial por sustitución
|
a lo que esta elevado, si lo derivo me da lo de afuera que mutiplica a la exponencial
|

|
|
trigonometricas por sustitución
|

|
|
|
Si f es una función continua en el intervalo [a,b] definiremos la integral definida de F como:
|

|
|
|
para evaluar las integrales definidas
|
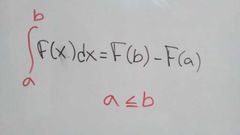
|
|
|
exacta
M(x,y)dx+N(x,y)dy=0 |
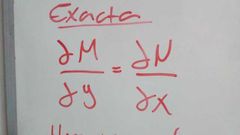
M respecto de y
N respecto de x {M(x,y)dx + g(y) |
|
|
pasos despues de {M(x,y)dx +g(y)
|
integro respecto a "x"
derivo respecto a "y" integro respecto a "y" |
|
|
Lineal (primer orden)
|
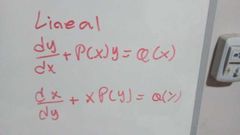
después reemplazamos en la formula
|
|
|
formula de p(x)
|
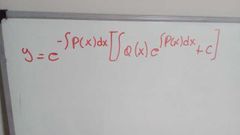
|
|
|
formula P(y)
|
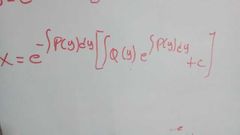
|
|
|
pasos despues de aplicar formula lineal
|
*integrar las integrales elevadas
*volver a integrar usando sustitución si es necesario *luego simplificar |
|
|
separables
|
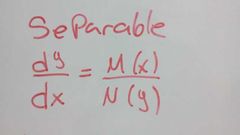
|
|
|
pasos para la separable
N(y) dy= M(x) dx |

|
|
|
Homogeneas (mismo grado)
|
función f(tx,ty)=t^nf(x,y)
|
|
|
ecuación Homogénea
|
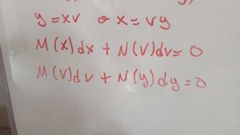
|